Circle Circumference Calculator | Calculate the Circumference
Articles, products, and services offered on this site are for informational purposes only. We are part of the Amazon Services LLC Associates Program, an affiliate advertising program. Amazon.com is compensated for sales resulting from links on our website.
Please review our disclaimer before acting based on anything you read or see.
The circumference of a ball is its observable outside perimeter when it is in your line of sight. So, to put it simply, circumference is nothing more than an object’s perimeter, whether round or elliptical. The idea is enjoyable not only for studying but also for teaching. This article introduces a very important and interesting concept: the circle circumference calculator.
The length of a circle’s circumference is likewise its circumference. The circle’s circumference may be calculated by cutting the circle open and measuring the length of the border.
Numerous points are distributed evenly around the center of a circle. And the point is referred to as the circle’s center. The radius of a circle is the separation between the center and any point along its circumference. The radius is always the same size. It stays the same.
The widest divergence possible between the ring places is regarded as a circle’s width. Its radius is twice as large. All of these often play a role in calculating the circle’s circumference. Come along as we highlight more on the Circle Circumference Calculator.
Circle Circumference Calculator
What is Circle Circumference?
The shape’s circumference defines the route or border that encircles any mathematics form. In other terms, the circumference is also known as the perimeter, which aids in determining how long a shape’s outline is. As we all know, a circle’s size and perimeter are its two most crucial characteristics.
The measurement of the circle’s boundaries is known as the circumference or perimeter of the circle. While the territory a circle covers is dictated by its area. The width of a horizontal path produced from the middle of a circle equals the perimeter of that circle. It is frequently defined in units like cm or unit m.
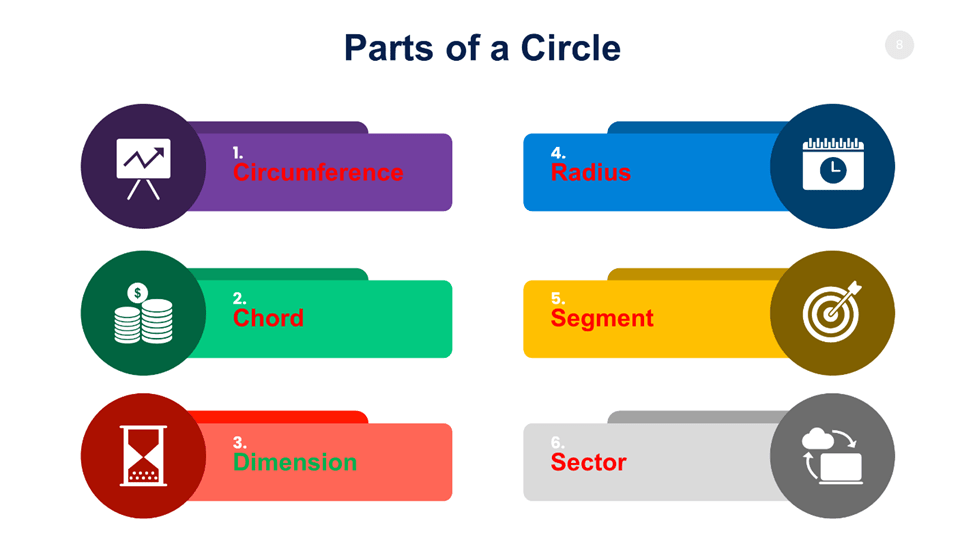
Parts of a Circle
Numerous items we encounter daily are ’round’ in form, including coins, bracelets, bottle caps, the Earth, wheels, etc. The circular form is often referred to as a circle in everyday speech. A circle is a closed plane figure made up of all the points equally spaced out from a fixed point in the same plane.
To put it another way, a circle is the locus of a point traveling on a plane while maintaining a constant distance from a fixed point. The circle’s radius is the constant distance from any point on the circle to its fixed point, referred to as the circle’s center. More circle components include:
Circumference
The circumference of a circle is its distance from its center. It may also be described as the circumference of a circle.
Chord
A chord is a linear line that connects two circumferential locations. Anywhere around the circle is possible for these two spots.
Dimension
A chord that traverses the circle’s center is referred to as the diameter. The largest chord you can draw in a circle is called a diameter.
Radius
A radius is a line that connects a point on the perimeter to the circle’s center. You could often see it represented as the letter “R” in the artwork.
Segment
A segment is a circle’s portion bounded by an arc and a chord. The fact that a segment resembles an orange segment makes it simple to recall what it is.
Sector
A sector is a circle’s portion bounded by an arc, two radii, and both. Sectors may also take the shape of quadrants. A sector is a simple concept to remember since it resembles pizza slices.
This can also be seen in the infographics below.
What is the Circumference of a Circle?
The size of a circle’s circumference is referred to as the circumference of a circle or the length of its edge.
Additionally, the Latin prefix circum-, which means “around or round around,” is used to produce the term circumference. As a result, any term created with this prefix refers to anything circular, either literally (such as the ring of a circus) or figuratively (such as an activity or the circumstances around somebody or something, such as their circumstances).
The circumference of a circle in mathematics refers to the length of the actual line enclosing it.
Methods to Find the Circumference
The following techniques may be used to determine the circumference:
Method 1:
Finding the proper formula is the first step in calculating the circumference. It would help if you used the following equation to get the circumference from the diameter:
C = PD
Let’s dissect this formula. Therefore, the letters “C” and “d” in this formula stand for circumference and diameter, respectively. Therefore, this formula means:
Circle diameter divided by its circumference equals p.
Pi, often known as *p, is a mathematical constant roughly equal to 3.14159. When employing pi in mathematics, 3.14 may be used instead.
Now that we are aware of the formula, we can begin to determine the circle’s circumference.
Method 2:
We cannot use a scale or ruler to measure the length of a circle since it is a curved surface. However, polygons like squares, triangles, and rectangles may be made this way. Instead, we may use a thread to calculate the circumference of a circle. Use the thread to trace the circle’s route, marking the spots as you go. A typical ruler may be used to measure this length.
Frequently Asked Questions
Is 3.14 the circumference of a circle?
Said PI is the ratio of a circle’s diameter to its circumference. It is represented as the Greek letter p or p. No matter how big the circle is, this proportion will always be equal to pi. The value of pi in decimal notation is around 3.14.
Is the circumference 3.14 times the radius?
A circle’s circumference is equivalent to pi times its diameter. Since the radius is 2 times the diameter, the formula for calculating a circle’s circumference using its radius is nearly twice pi times the radius.
How do you convert diameter to circumference?
A circle’s circumference may be determined by multiplying its diameter by p. (pi). You may also get the circumference by scaling 2radius by pi (p=3.14).
How is 3.14 calculated?
No matter what magnitude circle you drew, the result of dividing the circumference by the diameter is around 3.14. The ratio will never change, even if a bigger circle has a higher radius and circumference.
How do you calculate pi?
Pi is a ratio that may be calculated from a circle. The value of pi is given by p = Fractal dimension if the diameter and perimeter of a circle are known.
Is the diameter half a circumference?
The circumference of a circle is the length of a full “lap.” The diameter of a circle is also the length of the line segment that divides it in half. Consider the circle’s diameter and circumference as its inner and outside measurements.
What is the circumference of a 12-diameter circle?
You will apply the formula C=2pr to get a circle’s circumference; as a result, the circumference C is 2p6 38 inches.
What is the circumference of 1an 8-inch diameter?
Whenever the diameter is 18, the circle’s circumference equals 56.52 units.
What is the circumference of 3.5 diameters?
You will apply the formula C=2pr to get a circle’s circumference; as a result, the circumference C is 2p6 38 inches.
Why do we use 3.14 for Pi?
The distance from any point on a circle to its center or radius equals twice that distance. No matter what size circle you drew, the result of dividing the circumference by the width is around 3.14.
How do you calculate pi without a calculator?
Pi is a ratio that may be calculated from a circle. The value of pi is given by p = Circumference/Diameter if the width and perimeter of a circle are known.
What is the diameter of a 5-inch circumference?
Therefore, the circumference is given by C=5p 15. 708 inches if the diameter is 5 inches (3 DP)
Expert Opinion
A circle is a 2-D object made up of one point in the center of a circular, uninterrupted line. Every point on the line is precisely the same distance from the single point in the middle because of how the line is formed around it. A circle is defined as the central point, which is often implicitly marked, and the circumferential circle that surrounds it.
It might be difficult to determine a circle’s circumference. Thus, the Circle Circumference Calculator will aid you immensely.



Comments are closed.